■10進数

0 から 9 の10種類の値でデータを表現する。普段使用している数の表現であり、基数は、10である。
それぞれの桁は、9 の次に桁上がりが発生する。

■2進数

0 と 1 の2種類の値だけでデータを表現する。基数は、2である。コンピュータの内部では、電気信号（電気が流れている：ON、流れていない：OFF）の状態でしか情報を理解できないため、2進数で理解している。
それぞれの桁は、1 の次に桁上がりが発生する。

■16進数

0 から 9 の数字とA、B、C、D、E、F の文字を組み合わせてデータを表現する。基数は、16である。 2進数は、コンピュータでは理解しやすいが、桁が大きくなればなるほど人間には理解しづらい。そのため、桁数を少なく表示するために、2進表現を16進表現に変換することがある。
それぞれの桁は、以下の例のように桁上がりする。

■基数

数値を表すときに、各桁に重み付けをするが、その基本となる値を基数と呼ぶ。
10進数であれば、右から「一の位」「十の位」「百の位」と重み付けをするが、これらは「10の0乗の位」「10の1乗の位」「10の2乗の位」のように、各桁の重みを 10の累乗 で表すことができる。このときの10が基数である。
基数表記をする場合は、例のように数値の右下に書く。

■ビット

bit：binary digit。コンピュータが扱う情報の最小単位。
1ビットでは 0 と 1 の2通りの表現しか行うことができない。このビットを複数組み合わせて、情報を取り扱う。

■バイト

byte。8つのビットを、1つとして扱う単位。単位文字はB（大文字）。
1ビットで2通りの表現なので、1バイトでは 2⁸ ＝ 256通りの表現を行うことができる。

■BCDコード

Binary Coded Decimal。2進化10進コードとも呼ぶ。数値を、10進数文字列で表現するためのコード。
4ビットの2進数を用いて、10進数の1桁を表現する。ひとつの文字は、各2進数と同じだが、桁ごとに4ビットの2進数で表現するため、計算を行うときには数値に変換しなければならない。

■ゾーン10進数

2進数で10進数を表現する方式。1バイトで10進数1桁を表現する。
1バイトの中の上位4ビットを用いて、この1バイトが文字であることを示す。この上位4ビットをゾーン部という。ゾーン部の内容は各桁同じものだが、最後の桁だけは符号を表す値を入れる。

パック10進数と対比して、アンパック10進数と呼ばれることもある。

■パック10進数

2進数で10進数を表現する方式。4ビットで10進数1桁を表現する。
各桁にゾーン部を持たないため、ゾーン10進数と比べて、少ないバイト数で数値文字列を表現することができる。
パック10進数では、符号を最下位の4ビットで表現する。数値文字列がバイト単位で収まらなかった場合は、最上位4ビットに 0000 を格納する。

■補数

ある基数における数値に対し、その数を足すことで、ちょうど最上位桁が桁上がりする数を、その基数の補数という。

基数-1の補数では、もとの数を足すと、最上位桁の桁上がりに1足りない数になる。

基数2における補数（2の補数）は、負の数値の表現に用いられる。

■2の補数

負の2進数を表す方法のひとつ。
ある2進数のビット全てを反転して（1の補数）、それに1足したものが2の補数である。

コンピュータでは2の補数を使用して、負の数を加算することで、減算を実現している。

■固定小数点

小数点の位置を固定した表現。
小数点の位置は、コンピュータによって異なる。表現できる数値の幅は狭いが、誤差の発生しづらさや計算速度の速さなどの利点がある。

■浮動小数点

小数点の位置を固定しない表現。
数値を符号部、指数部、仮数部に分けて表現する。各部のビット数や基数、指数部の形式などは表現方式によって異なる。

数値によって小数点の位置を変えることができるので、表現できる数値の幅が広い。しかし、情報落ちなどの誤差に注意が必要である。

代表的な浮動小数点方式に、IEEE754やエクセス64がある。

■正規化

この単元では、浮動小数点方式における「正規化」について説明する。
仮数部の小数点位置を、表現方式で定められた位置に調整することを正規化という。正規化は、指数の調整によって行う。代表的な浮動小数点方式では、以下のような位置に調整する。

■バイアス

指数部を表す数値に加算する値。基準となる値（0）をあらわす。
2の補数表現を使わずに、正負の値を表現する方法であり、大小を単純に判断できる利点がある。
エクセス64方式のバイアスは、64である。

■論理シフト

全てのビットがそのまま左右に移動する方式。
シフトレジスタのビット数は限られているため、右にシフトしたときには右側のビットが、左にシフトしたときには左側のビットが、それぞれシフトした桁数分だけ失われる。
逆に、右側にシフトしたときには、左側に空きのビットができるが、そこには 0 が入る。左シフトのときも同様である。

■算術シフト

符号を考慮したシフト処理を行う方法。
符合を表すビット（先頭ビット：左端）をそのままにして、他のビットをシフトさせるため、シフト処理を実行しても符号が変化しない。
データの正負が正確であるので、数値の乗算（左シフト）や除算（右シフト）に使用する。

■オーバーフロー

桁あふれのことで、演算を行った結果、表現できる最大値を超えてしまう状態。
数値の表現に使用するビット桁数には限りがあり、あまりに大きな演算結果となった場合には、このような現象が発生する。

逆に、あまりに小さな演算結果となった場合には、アンダーフロー（下位桁あふれ）が発生する。

■ベン図

集合の関係を視覚的に表した図。外側の枠で全体を現し、その内側に各集合を円で表す。複数の集合の関係は、円の重なりで表す。
以下の図は、代表的な論理演算のベン図である。

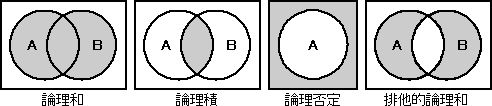
■論理演算

0 と 1 の2つの値で、論理和や論理積を行うこと。
このとき、0 と 1 を論理値といい、コンピュータのビットの状態に対応させている。

■真理値表

論理演算や論理回路の、全ての入出力の内容を表にしたもの。

■論理否定（NOT）演算

1つの値 A に対して行われる演算で、A の値が 1 のときの演算結果は 0 となり、A の値が 0 のときの演算結果は 1 となる論理演算である。コンピュータのビットで考えると、ビットの反転を行う論理演算となる。
論理否定は、否定するものにオーバーラインをつけて 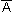としたり、 ¬A などで表す。

■論理和（OR）演算

2つの値 A、B に対して行われる演算で、2つの値のうち、どちらか一方でも 1 であるならば、演算結果は 1 となる論理演算である。両方とも 1 のときも 演算結果は 1となる。
論理和は、 A ＋ B、 A ∪ B、 A ∨ B などで表す。　「∪」は和の集合を表し、カップと読む。

■論理積（AND）演算

2つの値 A、B に対して行われる演算で、両方の値が 1 であるときのみ、演算結果が 1 となる論理演算である。他の値のときの演算結果は 0になる。
論理積は、 A ・ B、 A ∩ B、 A ∧ B などで表す。　「∩」は積の集合を表し、キャップと読む。

■NOR回路

論理回路のひとつで、OR回路とNOT回路を組み合わせた演算を行う。否定論理和とも呼ばれる。
演算結果は、OR演算を否定したものになり、2つの入力のうち、どちらか一方でも 1 であるならば、0 となる。2つの入力がどちらも 0 のときのみ 1 が出力される。
このNOR回路も、NAND回路と同じように、この回路の組み合わせだけで、論理積、論理和、論理否定の回路を実現できる。
この回路は、フラッシュメモリの構成にも利用されている。

■NAND回路

論理回路のひとつで、AND回路とNOT回路を組み合わせた演算を行う。否定論理積とも呼ばれる。
演算結果は、AND演算を否定したものになり、2つの入力がともに 1 のときのみ、0 となる。他の入力のときには 1 が出力される。
このNAND回路だけを組み合わせることで、論理積、論理和、論理否定の回路を実現できる。
この回路は、フラッシュメモリの構成にも利用されている。

■排他的論理和

2つの値 A、B に対して行われる演算で、どちらか一方の値だけが 1 であるときのみ、演算結果が 1 となる論理演算である。両方の値が 1 、または 0 で一致した場合の演算結果は 0になる。
排他的論理和は、A B と表す。
この原理を応用して半加算機の論理回路が成り立つ。

■半加算器

2つの入力信号を受けて、その和を出力する回路。排他的論理和回路を使用している。
演算結果と桁上がりの有り無し（キャリー）を出力する。
この回路が、コンピュータによる加算処理の基礎となっている。

■確率

ある事象（状態、出来事）が起こる確からしさを0（全く起こらない）から1（必ず起こる）の範囲の数値で表したもの。サイコロを１回ふって１が出る確率は1/6、1が出ない確率は5/6

■余事象

ある事象が起こらない状態を指す。

■確率の加法定理

２つ以上の事象が、排反事象（同時には起こりえない事象）のとき、いずれかが起こる確率は各々の確率の和で表すことができる。

■確率の乗法定理

２つ以上の事象が同時または続けて起こる確率を、各々の確率の積で表すことができる。

■期待値

事象によって得られる値の平均。値×確率の合計で求められる。

■マルコフ過程

直前に起こった事象のみによって次に起こる事象の確率が決定される特性をもつ過程

■メジアン

ひとまとまりの測定値を昇順（または降順）に並べたときの中央値

■モード

ひとまとまりの測定値のうち、もっとも出現頻度が高い値、最頻値

■偏差、分散、標準偏差

偏差：測定値と平均との差
分散：偏差の2乗の平均
標準偏差：分散の平方根

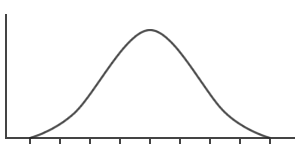
■正規分布

身長、成績などのように、平均近くの測定値が最も多く、平均から離れるほど測定値が少なくなる分布。グラフに表すと中央が高い左右対称の形になる。

■正規分布表

平均0標準偏差1の確率密度関数N(0,1²)を積分した値の一覧表。標準測度を用いて一般の正規分布 N(μ,σ²)の確率計算に応用できる。正規分布は連続型分布なのでP（χ＞測定値）とP（χ≧測定値）の値は等しい。

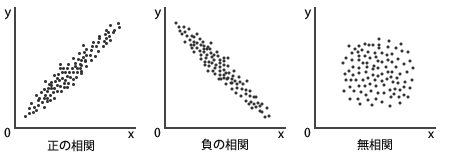
■正の相関、負の相関、無相関

散布図をもとに２つの項目の測定値の関係を回帰分析したとき、回帰直線が右上がりになるのが正の相関、右下がりが負の相関、回帰直線にあてはまるような関係がない場合は無相関という。

■稼働率

システムが故障することなく、正常に動作している時間の割合。システムの可用性・稼働性を評価する指標として使用する。
多くの場合稼働率は、まったく故障しない場合を 1 として、小数で表記する。（まったく故障しない場合を 100 としたパーセント表記をする場合もある）
稼働率は、MTBF（平均故障間隔）とMTTR（平均修理時間）を用いた、以下の式で計算することができる。

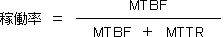
図の例で言うと、稼働率は、以下のようになる。

MTBF ＝ （ 50 ＋ 90 ＋ 130 ）÷ 3　＝ 90秒
MTTR ＝ （ 40 ＋ 30 ＋ 20 ）÷ 3　＝ 30秒
稼働率 ＝ 90 ÷ （ 90 ＋ 30 ） ＝ 0.75

■ガウスの消去法

連立一次方程式の解法の１つ。掃き出し法ともいう。

■指数

2×2×2＝2³ の3にあたる数、べき乗を表す。

■対数

3=log₂ 8　のとき、log₂ 8は2を底（てい）とする3の対数という。

■二分探索法

値の昇順（または降順）に並んだデータの中から求める値の位置を探索するアルゴリズムの一つ。平均比較回数と最大比較回数は対数を使って表現できる。バイナリサーチともいう。
一般に先頭の値から順に探索する逐次探索法よりも比較回数が少なくて済む。

■関数

F(x)の値が、xによって一意に決定するとき、F(x)はxの関数という。

■ハッシュ関数

関数F(x)から逆にxを求めることが困難なとき、この関数をハッシュ関数という。

■ニュートン法

関数F(x)=0の解の近似値を求める方法の一つ。